Zénon d’Élée est un philosophe grec ayant vécu de 490 à 430 avant Jésus-Christ, qui est fameux pour la formulation de différents « paradoxes » au sujet de l’espace et du temps.

Ces paradoxes, très connus notamment dans les mathématiques, ont été prétextes à des remarques très régulières, le plus souvent erronées car perdant de vue ou ne connaissant pas l’arrière-plan de la démarche de Zénon.

Zénon, disciple de Parménide et partisan de l’unité du monde, a en effet non pas tant à expliquer cette dite unité, qu’à rejeter comme faux les arguments de l’école de Pythagore – dont Platon est le plus grand représentant – considérant que l’Univers est composé d’unités quantifiables en tant que nombres.

Il raisonne ainsi sur le rapport entre le particulier et l’universel, en traitant spécifiquement de l’espace et du temps.

Zénon explique la chose suivante : s’il est vrai qu’il existe plusieurs choses particulières et non pas un simple universel – il n’utilise ni les termes de particulier ni celui d’universel, qui sont propres à nous – alors chaque chose particulière est séparée d’une autre chose particulière.

Mais pour être séparée, ces choses particulières doivent l’être par une chose particulière. Or, cette chose particulière séparant les deux autres doit également l’être d’une autre chose particulière, le processus étant infini.

Il en va de même si l’on utilise le principe de parties : chaque partie doit être séparée d’une autre par une partie, elle-même par une partie, etc., le processus étant infini.

Zénon oppose ainsi le nombre qui définit, circonscrit une partie de la réalité, et le fait que le principe de circonscrire est nécessairement infini dans son principe.

De manière plus simple, on peut prendre le paradoxe qu’il fait au sujet du lieu. Si toute chose est en un lieu, alors ce lieu est lui-même dans un lieu, qui lui-même est dans un lieu, le processus étant infini.

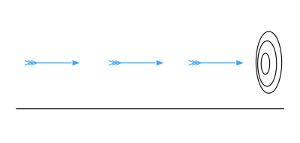
L’exemple de la flèche est tout à fait similaire : un arc lance une flèche. Si le temps est divisé en instants bien délimités, comment la flèche statique à cet instant passe-t-elle à un autre endroit à l’instant suivant ?

Comme on le voit, Zénon insiste sur la continuité générale de la matière, ce qui est pour nous le rapport entre l’universel et le particulier. Zénon a bien compris que si on utilise un monde matériel « mathématisé », on ne peut pas avoir de mouvement, qui pour nous avec le matérialisme dialectique est la contradiction de l’espace avec lui-même, produisant le temps.

Zénon a compris que le principe de dénombrement en unités du temps et de l’espace empêchaient une saisie de la continuité générale de la matière en mouvement.

Deux exemples très connus sont ici celui de la dichotomie et celui d’Achille et la tortue.

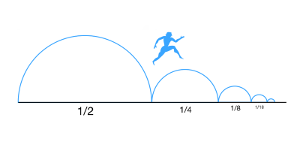
Dans celui de la dichotomie, Zénon dit qu’il lance une pierre. Imaginons qu’elle ait parcouru la moitié de son parcours. Elle va ensuite faire la moitié du parcours restant, et au cours de ce processus la moitié de ce parcours, et cela à l’infini.

Partant de là, la pierre ne fera jamais que la moitié de la moitié et cela à l’infini, n’avançant plus.

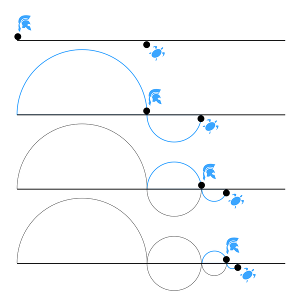
On a exactement le même exemple avec Achille poursuivant une tortue. Si l’on reprend l’exemple précédent, lorsqu’Achille a effectué la moitié du parcours pour la rattraper, il va faire la moitié du parcours restant, et ce à l’infini, ne rattrapant jamais la tortue.

Zénon modifie légèrement l’exemple en disant qu’Achille va à l’infini repasser par là où la tortue est passée.

Il est très ironique ici que les mathématiciens modernes, dans la logique de Pythagore, aient affirmé avoir trouvé la formule montrant qu’Achille rattrape bien la tortue (par le biais de la théorie des suites et des limites à l’infini), comme si Zénon ne le savait pas.

Les mathématiciens n’ont pas compris que Zénon dit que si le temps et l’espace sont interprétés avec des nombres allant à l’infini, alors l’espace entre Achille et la tortue est lui-même infini et Achille ne pourra jamais le parcourir.

Ils pensent s’en sortir avec le principe des suites, affirmant que même en accumulant des pas toujours plus petits, il y aura bien un moment où ils suffiront pour dépasser la tortue. C’est le principe de la convergence quand le nombre de pas tend vers l’infini, avec une valeur limite où la distance entre Achille et la tortue devient nulle.

Mais, Zénon sait très bien qu’Achille, dans les faits, dépassera la tortue. Ce qui l’intéresse, c’est de montrer que si on divise le temps et l’espace à l’infini de manière quantitative, tout en maintenant le principe de divisions en nombres de l’espace et du temps, alors le mouvement n’est pas possible, car on peut toujours ajouter des chiffres derrière un autre, comme par exemple 0,99999 à l’infini, ce qui fait qu’on ne parviendra jamais à 1.

Soit par conséquent on décide de cesser d’aller à l’infini – ce qui supprime l’infini – soit on considère que le temps est continu, qu’il n’est – et c’est ce que dit le matérialisme dialectique – qu’une expression de l’espace en contradiction avec l’espace, du mouvement.

Il n’y a pas de temps abstrait, de temps en soi. C’est pour cette raison que le paradoxe le plus intéressant est peut-être celui où se croisent trois « trains », c’est-à-dire plusieurs éléments à la suite.

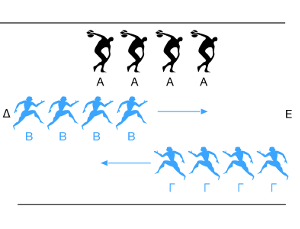
Si l’on prend l’exemple de trois trains de quatre coureurs, on a un train immobile et les deux autres trains se croisant à son niveau, car allant en sens contraire.

Ce qui se passe alors, c’est que le premier coureur du premier train en mouvement croise en même temps deux coureurs du train immobile et quatre du second train en mouvement.

Il a ainsi parcouru deux distances différentes ou bien, dit différemment, la moitié d’une durée est égale à cette même durée, puisqu’il a fallu le même temps pour croiser à la fois deux et quatre coureurs.

On comprend alors qu’en réalité se pose ici la question du référentiel, à laquelle ont contribué notamment Isaac Newton et Emmanuel Kant, c’est-à-dire du rapport entre l’espace et le temps, ce dernier étant le produit de la contradiction de l’espace avec lui-même.