Il existe en mathématiques l’addition, qu’on oppose à la soustraction, et la multiplication, qu’on oppose à la division. En réalité, addition et soustraction relèvent d’un seul même phénomène, uni par deux aspects contradictoires, tout comme multiplication et division formant un seul phénomène eux-mêmes.

Et le phénomène que représente l’addition et la soustraction, comme contradiction, produit le phénomène qu’est la multiplication et la division.

Une addition est concrètement une soustraction et une soustraction une addition. Si l’on dit que 2+3=5, on dit en même temps 5-3=2. Il s’agit de la même chose, mais inversée, comme vue à travers un miroir. On peut dire que l’addition est le reflet de la soustraction, ou inversement que la soustraction est le reflet de l’addition.

Cette dernière démarche semble plus juste, car tout reflet est nécessairement imparfait ou plus exactement asymétrique. Cela se voit avec le caractère remplaçable des nombres dans l’addition, qu’on ne retrouve pas dans la soustraction.

Dans l’addition, on a indifféremment 2+3=5 et 3+2=5. Or, pour la soustraction, on a d’un côté la même dimension remplaçable, mais sans aboutir au même résultat, puisque d’un côté 5-3=2, de l’autre 5-2=3.

La soustraction permet de revenir aux même fondamentaux que l’addition, mais en même temps elle est en décalage. On ne retrouve pas l’identité entre 3 et 2 qu’on a dans l’addition : 2 et 3, dans la soustraction, restent différents, malgré leur liaison.

C’est en ce sens qu’on peut dire que la soustraction est le reflet asymétrique de l’addition.

La multiplication et la division découlent, comme phénomène contradictoire, de cette contradiction addition/soustraction. Cela se voit dans les caractéristiques qu’on y retrouve.

Si l’on prend la multiplication, on a indifféremment 5×2=10 ou 2×5=10. Dans la division, on a 10:2=5 et 10:5=2. On a pareillement l’identité dans la multiplication, comme dans l’addition, et la différence dans la division, comme dans la soustraction. 2 et 5 sont remplaçable dans la multiplication, pas dans la division.

Ce qui change par contre pour la multiplication/division par rapport à l’addition/soustraction, c’est que la première relève de la qualité, la seconde de la quantité.

Dans l’addition comme la soustraction, on fonctionne suivant le principe de l’accumulation. On peut tout à fait remplacer un chiffre par des bâtonnets, on est dans un calcul très facile à saisir pour l’esprit puisqu’on ajoute, on retranche et qu’on peut le faire sans interruption aucune, en continuité.

On a ainsi I I I I I auquel on enlève II, ce qui donne I I I, auquel peut ajouter I I I I I ce qui donne I I I I I I I I ; on peut ajouter, soustraire, on s’y retrouve très facilement.

Cela n’est pas vrai pour la multiplication et la division. Pour le comprendre, on peut s’appuyer sur la légende de la naissance du jeu d’échecs en Inde. Ayant inventé le jeu pour le roi, Sissa demanda qu’on lui fournisse du riz de la manière suivante : un grain de riz pour la première case du jeu, deux pour la seconde, quatre pour la troisième, huit pour la quatrième, et ainsi de suite.

Sur le plan mathématique, Sissa a demandé qu’on double le nombre de grains de riz à chaque case. Le roi accepta la demande, sauf que si on double le grain de riz depuis la première case jusqu’à la soixante-quatrième, on obtient au final plus de 18 milliards de milliards de grains de riz.

Le roi avait raisonné en termes d’addition, pensant que le processus correspondrait à 1, 1+1, 2 +2, 4+4, 8+8,16+16, etc. et que cela n’irait pas bien loin. En réalité, il s’agissait du passage de la quantité à la qualité, de l’addition à la multiplication.

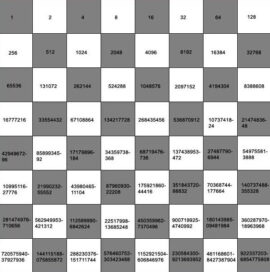
Cela se comprend si on regarde l’échiquier dans son ensemble. Si l’on prend deux cases qui se suivent, on reste dans l’addition. Mais dès qu’on voit les chiffres, on constate qu’on est dans des proportions propres à la multiplication.

Voici justement quelques exemples de multiplications qu’on retrouve au travers des nombres qui doublent. On ainsi 32×8192=262144, 4096×8388608=34359738368, etc.

Ce qui est cohérent puisqu’on double à chaque fois, qu’il s’ensuit la mise en place d’une proportion et que la multiplication reflète cette proportion. Autrement dit, lorsqu’on double à chaque fois, procédant à une addition de deux nombres identiques, il s’ensuit un rapport entre les nombres qui sont le produit de cette addition, qu’on retrouve sous la forme de proportion visible dans la multiplication.

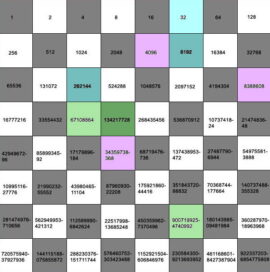
L’erreur du roi en Inde consistait précisément à s’en tenir à un développement linéaire – accumulatif, là où en réalité le mouvement d’addition connaissait un saut qualitatif aboutissant à un développement inégal procédant par bonds.

C’est un excellent exemple de comment la multiplication/division est issue de l’addition/soustraction, par l’établissement de nouveaux rapports, de nouvelles liaisons internes.