Le matérialisme dialectique considère que rien ne peut être statique, en équilibre, symétrique. Il y a forcément une nuance, une différence, une lutte, une contradiction, une transformation. C’est là qu’on comprend qu’il faut accorder une importance fondamentale au développement inégal, bien plus que cela ne l’a été fait au 20e siècle.

Le carré présente ici un défi puissant. En effet, dans un carré, on semble chercher en vain une transformation, une contradiction, une lutte, une simple différence, ou même juste une nuance.

Les côtés a, b, c, d d’un carré ont la même taille. Ils sont bien entendu différents, cependant ils ont une identité substantielle : on peut indifféremment les remplacer l’un par l’autre. On ne peut pas fonder une identité réelle, une différence authentique, simplement là-dessus.

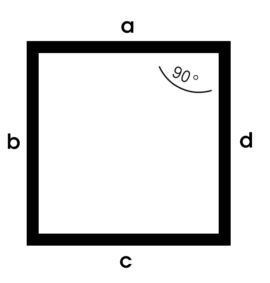
Les angles sont pareillement tous de 90°. On a beau chercher, on ne trouve rien ! Il faut bien pourtant que le carré obéisse à la dialectique !

La solution est la suivante. La contradiction du carré tient à celle entre le tout et les parties. Ce n’est pas tant que les côtés du carré soient différents qui comptent, que le fait qu’il faille passer de l’un à l’autre. Ce passage est discontinu. C’est là l’aspect qualitatif.

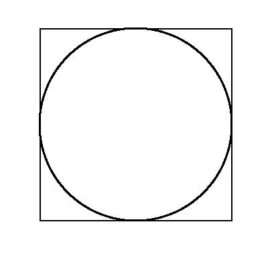
Et quel est l’opposé du carré ? C’est le rond, justement. Car chez lui, il n’y a pas cette discontinuité ! On passe en effet d’un point à un autre, sans rupture. Par contre, ce n’est pas en suivant une ligne que l’on « progresse », mais justement de manière discontinue.

Inversement, il n’y a pas de contradiction entre le tout et les parties !

Ainsi, le carré voit sa contradiction se poser entre le tout et les parties, la discontinuité se situant au niveau du passage d’un côté à un autre. Là est la différence permettant la lutte.

Le rond voit quant à lui sa contradiction se poser dans le mouvement des points, qui n’est pas linéaire, qui n’est pas continu : il ne s’agit en effet pas simplement d’un point ajouté après un autre, mais d’une ligne connaissant une tendance à la courbe. Il n’y a par contre pas d’opposition entre le tout et les parties.

Et les deux sont des opposés, dans une opposition correspondant à la contradiction entre le tout et les parties qui s’oppose à la discontinuité linéaire.